Maybe I should start explaining what a metric is. Or curvature. Or the energy-stress tensor...
Nahhh... :)
Let's run before walk with an example. It's funnier this way.
Legend says Karl Schwarzschild was a german artillery officer during WWI, but the truth is he was a physicist and astronomer before that. He died several months after finding the first analytical solution to EFE's, of an illness called Pemphigus (click at your own risk). You have read right: Schwarzchild did find an analytical solution to Einstein Field Equations. Exactly. Analytically. Manly.
Truth be said, he did it for the "simplified" case of a spherical static object, but it's a good aproximation, specially for people like me who need to learn. Are you ready? I prevent you I have (finally) learned how to use latex in blogger...
We start with our old friends, EFE's, with $\Lambda = 0$ because we are not really into an expanding the universe (for now). People sometimes refers to this as a vacuum solution condition, but a vacuum solution is actually stating that apart from the spherical mass which is the cause of curvature, there is no more energy or mass around. Anyway, that yields...
\begin{equation}
R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=\frac{8\pi~G}{c^4}T_{\mu\nu} ~~\text{with}~~ \nu=0..3, \mu=0..3
\end{equation}
\begin{equation}
R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=\frac{8\pi~G}{c^4}T_{\mu\nu} ~~\text{with}~~ \nu=0..3, \mu=0..3
\end{equation}
That is 16 equations. Let's focus. What do we know? What we do "know" here is the stress-energy tensor $T_{\mu\nu}$. We are assuming a perfect spherical mass in the center of coordinates, with no velocity and no variation with time at all. So... Suprise...
\begin{equation}
T_{\mu\nu} = \left (
\begin{array}{cccc}
T_{00} & T_{01} & T_{02} &T_{03} \\
T_{10} & T_{11} & T_{12} &T_{13} \\
T_{20} & T_{21} & T_{22} &T_{23} \\
T_{30} & T_{31} & T_{32} &T_{33}
\end{array}
\right ) = \left (
\begin{array}{cccc}
0 & 0 & 0 &0 \\
0 & 0 & 0 &0 \\
0 & 0 & 0 &0 \\
0 & 0 & 0 &0
\end{array}
\right )
\end{equation}
Ok. It's zero. All of it. For the moment, let's have an eye on $T_{\mu\nu}$ in order to understand what does this mean.
A stress-energy tensor defines density and flux of energy and momentum in spacetime.
From wikipedia. Meaning of elements in stress-energy tensor. You say contravariant, I say covariant. It doesn't matter for now :)
As you can see, outside the spherical mass, there is nothing (well, there is something called gravitational energy, too spooky for now and EFE's don't account for it). In our case, there is no momentum, there is no pressure, there is no energy outside the sphere (we said this was a vacuum solution); so it makes perfect sense: energy-stress tensor is zero. What's the source of curvature, then? Well, obviously it's the mass of the sphere and it shall be accounted in other place. If we were inside the sphere, then $T_{\mu\nu} \ne 0$, but we are not, are we? Well, we are not :)
Coming back to the equations, we have now something like this.
\begin{equation}
R_{\mu\nu}-\frac{1}{2}Rg_{\mu\nu}=0 ~~\text{with}~~ \nu=0..3, \mu=0..3
\end{equation}
We are going to find the metric, which we can define as the way the spacetime is, under the effects of a certain stress-energy tensor.
Now, I know what are you thinking. You probably thought the point in this solution was finding Ricci tensor (curvature) elements. Well, it turns out Ricci tensor elements and metric elements are more than related.
\begin{equation}
R_{\mu\nu}= R^{\beta}_{\mu\nu\beta}= \Gamma^{\beta}_{\mu\beta,\nu}- \Gamma^{\beta}_{\mu\nu,\beta}+\Gamma^{\alpha}_{\mu\beta}\Gamma^{\beta}_{\alpha\nu}-\Gamma^{\alpha}_{\mu\nu}\Gamma^{\beta}_{\alpha\beta}
\end{equation}
\begin{equation}
R_{\mu\nu}= R^{\beta}_{\mu\nu\beta}= \Gamma^{\beta}_{\mu\beta,\nu}- \Gamma^{\beta}_{\mu\nu,\beta}+\Gamma^{\alpha}_{\mu\beta}\Gamma^{\beta}_{\alpha\nu}-\Gamma^{\alpha}_{\mu\nu}\Gamma^{\beta}_{\alpha\beta}
\end{equation}
And, as you may suspect, all those Christoffel symbols can be written as:
\begin{equation}
\Gamma^{\mu}_{\nu\sigma}=\frac{1}{2}g^{\mu\lambda}\left \{g_{\lambda\nu,\sigma}+ g_{\lambda\sigma,\nu}+g_{\nu\sigma,\lambda}\right \}
\end{equation}
\begin{equation}
\Gamma^{\mu}_{\nu\sigma}=\frac{1}{2}g^{\mu\lambda}\left \{g_{\lambda\nu,\sigma}+ g_{\lambda\sigma,\nu}+g_{\nu\sigma,\lambda}\right \}
\end{equation}
So, if we find the metric, we find it all!!
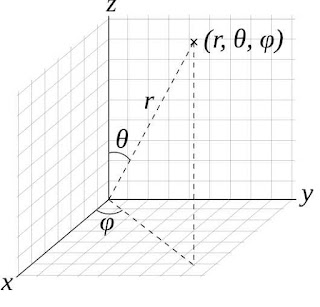
Good news is only diagonal Ricci elements remain (we will see that later), which will lead us to solve only 3 or 4 equations in order to find the metric elements. Another good news is Schwartzchild, actually knew what did the metric look like. He did it by defining polar spherical coordinates in the problem. Well, not sure if he did, but we are going to do it :)
A polar spherical coordinate system. From wikipedia. Spherical coordinates help to achieve symmetries. We will have to pay the price of non orthogonal coordinate axis, but it is actually worth it.
For a boring, flat, rectangular metric, we will have the form...
\begin{equation}
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = dt^2-dx^2-dy^2-dz^2
\end{equation}
Which is almost the same in spherical coordinates.
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = dt^2-dx^2-dy^2-dz^2
\end{equation}
Which is almost the same in spherical coordinates.
\begin{equation}
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = dt^2-dr^2-r^2d\theta^2-r^2sin^2\theta d\varphi^2
\end{equation}
The elements $r^2$ and $sin^2\theta$ appear because of choosing a non orthonormal coordinate frame of reference. A variation in $\theta$, for instance, has to account for a variation in $r$, in order to remain orthogonal. They are called metric factors and you probably have already seen them if you have solved any equation system in non rectangular coordinates. So, is it solved? We have found the metric factors cheating and choosing a polar spherical coordinate system. Well, no.
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = dt^2-dr^2-r^2d\theta^2-r^2sin^2\theta d\varphi^2
\end{equation}
The elements $r^2$ and $sin^2\theta$ appear because of choosing a non orthonormal coordinate frame of reference. A variation in $\theta$, for instance, has to account for a variation in $r$, in order to remain orthogonal. They are called metric factors and you probably have already seen them if you have solved any equation system in non rectangular coordinates. So, is it solved? We have found the metric factors cheating and choosing a polar spherical coordinate system. Well, no.
We did it for flat space.
For a sphere of mass M, we have to work a little more...
\begin{equation}
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = Adt^2-Bdr^2-Cr^2d\theta^2-Dr^2sin^2\theta d\varphi^2
\end{equation}
\begin{equation}
ds^2=\sum_{\mu\nu}g_{\mu\nu}dx^{\mu}dx^{\nu} = Adt^2-Bdr^2-Cr^2d\theta^2-Dr^2sin^2\theta d\varphi^2
\end{equation}
We have A, B, C and D as final unknown functions or constants. Actually...
\begin{equation}
\begin{array}
gg_{tt}=g_{00} = A\\
g_{rr}=g_{11} = B\\
g_{\theta\theta}=g_{22} = Cr^2\\
g_{\varphi\varphi}=g_{33} = Dr^2sin^2\theta
\end{array}
\end{equation}
For now, we have ended. The only work that remains to be done in order to solve the metric is:
\begin{array}
gg_{tt}=g_{00} = A\\
g_{rr}=g_{11} = B\\
g_{\theta\theta}=g_{22} = Cr^2\\
g_{\varphi\varphi}=g_{33} = Dr^2sin^2\theta
\end{array}
\end{equation}
For now, we have ended. The only work that remains to be done in order to solve the metric is:
- Justify why we should only account for diagonal terms in Ricci tensor (and diagonal terms in the metric tensor)
- Apply last expressions for $g_{\mu\nu}$ into the $R_{\mu\nu}$ equation.
- Find the value for A, B, C and D and finally give the metric.
But that's work for the next post :)
Edit: A couple of mistakes, actually, regarding grammar and math. Sorry. :)

No comments:
Post a Comment